Scopri cos’è una funzione lineare e come viene rappresentata
In matematica, le funzioni determinano il tipo di relazione che due elementi o variabili hanno tra loro. Pertanto, sono molto utili per descrivere i fenomeni, specialmente in aree come Finanza, Statistica, Ingegneria, Medicina, Economia, tra gli altri. Oggi vogliamo dedicare questo articolo a parlare di cos’è una funzione lineare e di come viene rappresentata . Quindi vi invitiamo a leggerlo se questo argomento è di vostro interesse.
Per chiarire i tuoi dubbi, abbiamo preparato questo articolo. Resta con noi e scopri cos’è una funzione lineare.
Che cos’è una funzione lineare e come viene rappresentata?
All’interno della geometria analitica e dell’algebra, è nota come funzione polinomiale di primo grado rappresentata come segue:
f(X) = mX + b
Se analizziamo l’espressione, vediamo come quando si ha il valore di “X”, la prima cosa da fare è moltiplicarla per “m” e sommare il prodotto a “b”. Pertanto, il risultato di tutta questa operazione sarà il valore di f di “X” (f (X)).
Le funzioni lineari sono molto utili per calcolare i fenomeni che si verificano nella vita di tutti i giorni. Ad esempio, attraverso questa funzione è possibile determinare il costo dei servizi di base come acqua, luce o gas. Oltre all’importo, sarà possibile tenere conto della proporzione in caso di aumenti.
Tra le caratteristiche che si possono citare di una funzione lineare ci sono:
- La sua rappresentazione nel piano cartesiano corrisponde ad una retta (motivo per cui è nota come funzione lineare).
- “m” rappresenta un valore di cambiamento, mentre “b” è una costante.
Elementi della funzione lineare
Considerando la sua forma di espressione f (X) = mX + b, gli elementi che lo compongono sono:
- “X”: variabile indipendente (il suo valore non dipende da nessun’altra variabile e può essere assegnato liberamente).
- f (X): in alcuni casi è rappresentato con il simbolo “y”. Corrisponde alla variabile dipendente (il suo valore dipende da “X”).
- “m”: si riferisce alla pendenza , che determina il grado di inclinazione della linea.
- “b”: è noto come origine e corrisponde all’asse di taglio.
Forme di rappresentazione della funzione lineare
Come abbiamo visto attraverso un’espressione o una formula, è usata per rappresentare una funzione lineare, tuttavia, questo processo è possibile anche attraverso una tabella o un grafico.
Per rendere più chiaro cos’è una funzione lineare e come viene rappresentata , facciamo un esempio.
TAVOLO
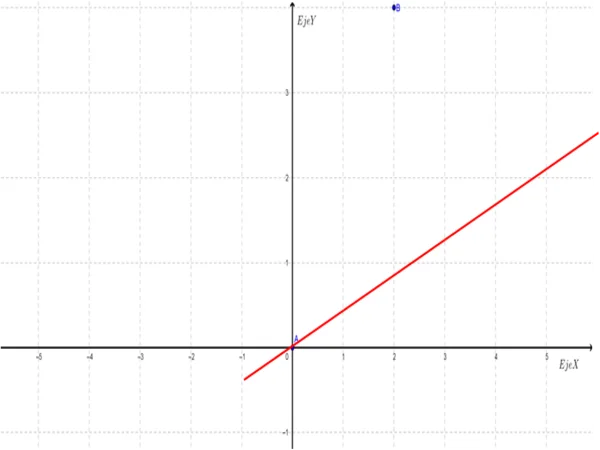
Abbiamo la seguente funzione: f (X) = 2X + 0
Sulla base di questa formula è possibile determinare quale tabella e quali valori devono essere registrati.
|
X |
Y |
|
0 |
0 |
|
2 |
4 |
|
4 |
8 |
Qui, i valori di “X” sono stati designati arbitrariamente, mentre quelli di “y” hanno avuto origine dal calcolo di un’equazione lineare :
y = mX
Quindi, il primo valore viene calcolato dalla moltiplicazione di “m” = 2 per “X” = 0.
y = 2*0
= 0
Mentre il secondo è calcolato da “m” = 2 da “X” = 2. Rimangono come segue:
y = 2*2
= 4
Osservando la tabella e nell’operazione vediamo come i valori rappresentano punti che possono trovarsi nel piano cartesiano.
rappresentazione cartesiana
Quando rappresentiamo graficamente , prendiamo i valori ( x, y ) mostrati nella tabella, o quelli ottenuti attraverso l’operazione e rappresentiamo.
UN = (0,0)
B = (2,4)
C = (4.8)
Come si vede, si forma una retta lineare con crescita proporzionale, il che significa che è una funzione costante dove l’aumento del valore di “ x ” è proporzionale al valore di “ y ”.
Come ogni aspetto della matematica, le funzioni lineari sono applicabili nella realtà. Per questo motivo, ti invitiamo a formarti in quella che sarebbe una business school specializzata, dove puoi conoscere questo e altri argomenti correlati.
Scopri cos’è una funzione lineare e come viene rappresentata
Approfondisci la tua conoscenza di cos’è una funzione lineare e di come viene rappresentata attraverso i corsi di Matematica e Statistica disponibili sulla piattaforma digitale Euroinnova , la nostra business school specializzata nella formazione online.
Se entri subito, otterrai uno sconto eccezionale.